Zonotiles are
centrally-symmetrical convex polygons (zonogons) tiled
by smaller zonogons. 
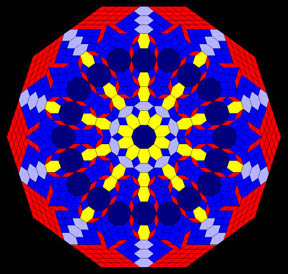
They are related to
quasicrystals and Penrose tilings. However, a zonotile may be
strongly symmetrical, as in the image above, or those below. The
two zonotiles below are of special interest, because they contain
patches of semi-regular Archimedean tessellations. 
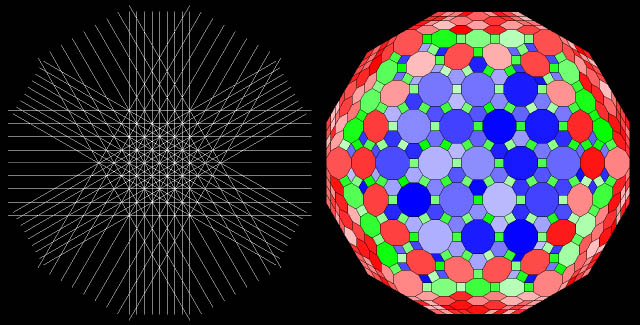
An "Archimedean" zonotile with its corresponding line arrangement.
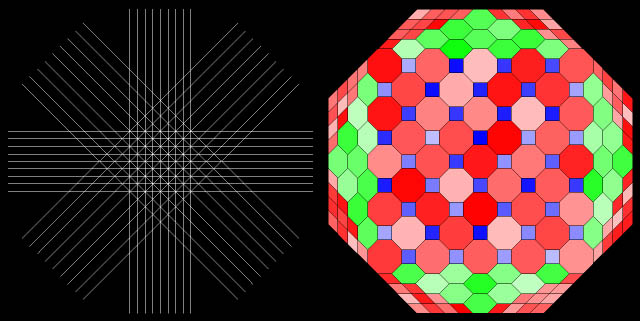
An "Archimedean" zonotile with its corresponding line arrangement.
Although zonotiles may exhibit strong n-fold rotational
symmetry, one may obtain patches which exhibit quasiperiodic order,
as in the image below.
The above images were made using the software Mathematica.
I adapted an algorithm written in PostScript, in which what is
called the generalized dual method is implemented. In this method,
sets of parallel lines are constructed, typically, parallel to
the sides of some regular polygon. The line sets intersect one
another in many places. If some k of the lines intersect
at a single point, a 2k-gon is made; then again, if some
k of the lines bound a given region, k zonogons
will meet there. However, we are not exactly constructing the
dual of the line arrangment. Suppose there are 5 sets of 7 lines,
35 lines altogether. The lines are expressed in the form {x,y,d},
where {x,y} is the normal, d, the distance from the origin. For
each of the 35 lines, we associate that line with every possible
pair of lines, and find the sign of the determinant of these three
3-vectors. We obtain a list of "sign vectors" composed
of 35 -1's, 0's, and 1's. These provide a code used to draw the
actual tiles.
Download the Mathematica
notebook.