

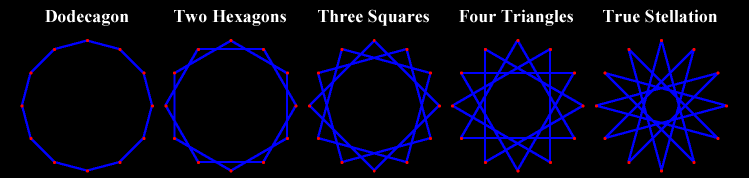
We stellate an n-dimensional polytope by producing the (n-1)-dimensional polytopes which bound it, until they intersect. Sometimes the new bounding-polytopes-of-intersection define, not a single new polytope, but a compound of polytopes. This is well illustrated by the stellations of the regular dodecagon, below. Only one yields a star polygon; the others are just compounds of hexagons, squares and triangles. Technically, since the same vertices are used in these various stellations, this is the faceting of the dodecagon, not its stellation. The results are the same, here. Stellation and faceting do not give equal results with most polyhedra ot polytopes, but do with regular polygons, since these figures are self-dual.
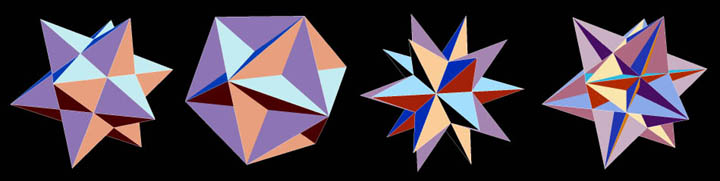
The Kepler-Poinsot polyhedra, from the left: the small stellated dodecahedron {5/2, 5}; great dodecahedron, {5, 5/2}; great stellated dodecahedron, {5/2, 3}; and the great icosahedron, {3, 5/2}.
The first three are stellations of the Platonic
dodecahedron, the fourth, the only regular stellation (of 59)
of the Platonic icosahedron.
The above non-convex polyhedra are stellations of convex polyhedra. The theory of stellation is quite interesting (see a comparison of three primitive operations on convex polyhedra: completion, stellation, and faceting), and of the many devotees of things polyhedral, and things polytopical, many are more or less obsessed with stellation. Much of what makes the subjects of polyhedra and polytopes so compelling, is symmetry. When one moves from the convex polyhedra, to stellations, additonal layers of great subtlety and complexity pose a tremendous challenge, one which might not be fully met within a lifetime. That this is so is partly evidenced by the very name of the Kepler-Poinsot solids, the only regular star polyhedra. Johannes Kepler, a very able and determined student of polyhedra, discovered the great and smalled stellated dodecahedra, but two centuries passed before Poinsot found the great dodecahedron and great icosahedron!
There is still much to be learned about stellations. Part of what inhibits rapid progress in this area, is the difficulty in constructing accurate models. The faces interpenetrate, and one must calculate the cut out the obscure shapes of exposed "facelets." Some of this difficulty bleeds over into the digital world: 3D rendering engines on modern personal competers (ca. 2000) are often hard-pressed to accurately render thousands of intersecting polygons.
Here is an excerpt from Chapter 6 of H.S.M. Coxeter's Regular Polytopes:
6.2. Stellating the Platonic solids. Just as the definition of a polygon can be generalized
by allowing non-adjacent sides to intersect, so the definition
of a polyhedron can be generalized by allowing non-adjacent faces
to intersect; and it is natural at the same time to allow the
faces to be star polygons. We proceed to describe four such polyhedra,
which are regular according to the definition in Chapter 2.1:
the small stellated dodecahedron {5/2, 5} and the great stellated
dodecahedron {5/2, 3}, whose faces are pentagrams (five or three
at each vertex); and their respective reciprocals, the great dodecahedron
{5, 5/2} and the great icosahedron {3, 5/2}, whose vertex figures
are pentagrams. We can construct these "Kepler-Poinsot polyhedra"
by stellating or faceting the ordinary dodecahedron and icosahedron.
The Great Icosidodecahedron
If star polyhedra, in merely three dimensions, pose a challenge, how much more so the star polytopes in higher space! It is perhaps fortunate that no regular star polytopes exist in more than four dimensions. In 4-space there are ten, all with the "extended icosahedral group" symmetry, of order 14,400. The icosahedral group is a subgroup, and thus both solid sections, and projections into polyhedra, can have icosahedral symmetry. Constructions for all of these, along with plane and solid projections, and solid sections, are provided in my "Regular Polytopes" Mathematica notebook. A plane projection of {5/2, 3, 3} appears near the top of my Polytopes page. Check out George Olshevsky's pages on four-dimensional polytopes. George is investigating the uniform polytopes in four dimensions, many of which are star polytopes.
Back to Russell Towle's homepage.