
Mathematica is the world's premier mathematical software. Not only does it have a wealth of built-in, highly optimized mathematical functions, but it is also a programming language, and thus, one can contrive one's own functions. It has beautiful PostScript graphical output, and allows typeset-quality mathematical notation. This very remarkable program was pioneered by Stephen Wolfram, and developed with the help of many others, notably Roman Maeder and Theodore Gray.
My own introduction to Mathematica was in 1988, I believe, when word came that it would be ported to the Macintosh operating system. I saw the debut of the Mac version at MacWorld Expo in San Francisco, in 1989. Its 3D graphics were of special appeal to me, but for years I lacked a computer powerful enough to run the program. Finally, about 1995, I got my foot in the door.
At that time I had been programming in BASIC for several years, beginning with a Commodore Plus 4 in 1987, and continuing with a Mac Plus, and then a Mac Classic. I had devised algorithms to construct the polar zonohedra, of arbitrary complexity and proportion, and perform parallel projections onto an arbitrary plane. I could make animations of rotations, and also devised algorithms to construct what I call "expansions" of polar zonohedra. Mathematica posed quite a challenge at first.
Pursuing the challenge, I continued working
with polar zonohedra, and branched out into curious variants I
discovered, naming them spirallohedra, and eventually tackled
the regular polytopes in four dimensions. Several of my notebooks
may be downloaded below. You will need Stuffit
Expander (Mac or Windows version) to decompress the notebooks.
An n=5 rhombic spirallohedron.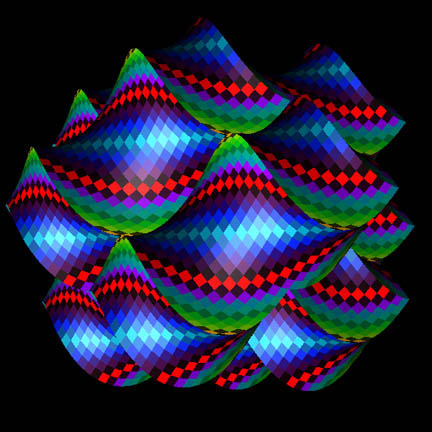
A close-packing of rhombic spirallohedra.
Download the
Spirallohedra notebook (needs Stuffit Expander to decompress)
The dodecahedral expansion of a polar zonohedron.
A skew dodecahedral expansion of a polar zonohedron.
Download the Expansion
notebook (needs Stuffit Expander to decompress)
A parallelogrammic/rhombic helicoid. The faces have been sorted by surface area and colors assigned to each subset.
Download the Helicoid
notebook (needs Stuffit Expander to decompress)
3D zonotiles; above, an edge=3 zonotile based upon the truncated icosidodecahedron, in which only some of the zonohedral tiles were displayed. leaving gaps and holes. Below, the same zonotile, with an equatorial region of the zonohedra displayed. Note the truncated icosidodecahedron (an Archimedean solid) in the center.
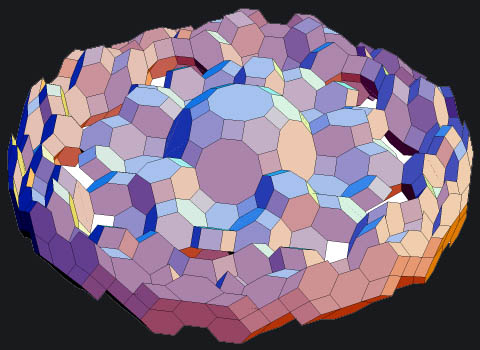
Download the 3D Zonotile notebook (needs Stuffit Expander to decompress)

Above: A hidden-detail-removed, cube-first
projection of the truncated 24-cell, {3,4,3}. Note that this induces
a tiling of a zonohedron by smaller zonohedra: a 3D zonotile.
Created using my Regular Polytopes notebook, rendered in
POV-Ray.
A vertex-first projection of the regular four-dimensional star polytope, {3,3,5/2}, into a 3-space.
Download the Regular Polytopes notebook (needs Stuffit Expander to decompress)
A "star" polar zonohedron, in which the usual cyclic ordering which characterizes a convex polar zonohedron (or convex regular polygon) was abandoned, and the ordering which characterizes a regular star polygon substituted. When the ordering is such that a compound of polygons would occur, instead of a star polygon, "bead" zonohedra arise.
Download the StarBead notebook (needs Stuffit Expander to decompress)
Download the Zonohedral Completion notebook (needs Stuffit Expander to decompress)
Download the 2D Zonotiles notebook (needs Stuffit Expander to decompress)